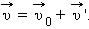1.2. Относительность движения

Движение тел можно описывать в различных системах отсчета. С точки зрения кинематики все системы отсчета равноправны. Однако кинематические характеристики движения, такие как траектория, перемещение, скорость, в разных системах оказываются различными. Величины, зависящие от выбора системы отсчета, в которой производится их измерение, называют относительными.

Пусть имеются две системы отсчета. Система 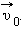XOY условно считается неподвижной, а система X'O'Y' движется поступательно по отношению к системе XOY со скоростью  Система XOY может быть, например, связана с Землей, а система X'O'Y' – с движущейся по рельсам платформой (рис. 1.2.1).

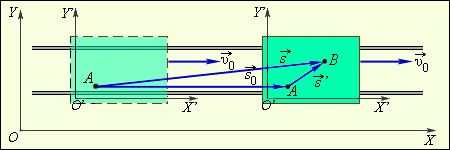Рисунок 1.2.1. Сложение перемещений относительно разных систем отсчета

Пусть человек перешел по платформе за некоторое время из точки 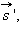A в точку B. Тогда его перемещение относительно платформы соответствует вектору  а перемещение платформы относительно Земли соответствует вектору  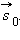Из рис. 1.2.1 видно, что перемещение человека относительно Земли будет соответствовать вектору  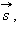представляющему собой сумму векторов  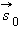и 

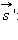
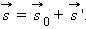В случае, когда одна из систем отсчета движется относительно другой поступательно (как на рис. 1.2.1) с постоянной скоростью 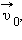 это выражение принимает вид: 

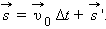Если рассмотреть перемещение за малый промежуток времени Δt, то, разделив обе части этого уравнения на Δt и затем перейдя к пределу при Δt → 0 получим: 

(*)

Здесь 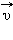 – скорость тела в «неподвижной» системе отсчета 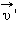XOY,  – скорость тела в «движущейся» системе отсчета 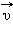X'O'Y'. Скорости  и 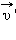 иногда условно называют абсолютной и относительной скоростями; скорость  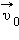называют переносной скоростью.

Соотношение (*) выражает классический закон сложения скоростей: 

Абсолютная скорость тела 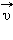 равна векторной сумме его относительной скорости  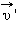и переносной скорости  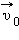движущейся системы отсчета.

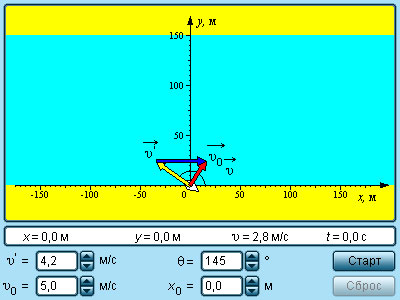Модель. Относительность движения

Следует обратить внимание на вопрос об ускорениях тела в различных системах отсчета. Из (*) следует, что при равномерном и прямолинейном движении систем отсчета друг относительно друга ускорения тела в этих двух системах одинаковы, т. е. 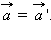 Действительно, если  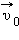– вектор, модуль и направление которого остаются неизменными во времени, то любое изменение  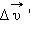относительной скорости тела будет совпадать с изменением  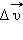его абсолютной скорости. Следовательно, 

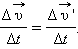Переходя к пределу (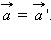Δt → 0), получим 

В общем случае, при движениях систем отсчета с ускорением друг относительно друга, ускорения тела в различных системах отсчета оказываются различными.

В случае, когда вектора относительной скорости 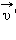 и переносной скорости  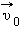параллельны друг другу, закон сложения скоростей можно записать в скалярной форме: 

υ = υ0 + υ'.

В этом случае все движения происходят вдоль одной прямой линии (например, оси OX). Скорости υ, υ₀ и υ' нужно рассматривать как проекции абсолютной, переносной и относительной скоростей на ось OX. Они являются величинами алгебраическими и, следовательно, им нужно приписывать определенные знаки (плюс или минус) в зависимости от направления движения.