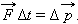1.16. Импульс тела
Пусть на тело массой 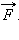 Под действием этой силы скорость тела изменилась на
Под действием этой силы скорость тела изменилась на 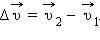 Следовательно, в течение времени
Следовательно, в течение времени
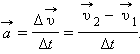 |
Из основного закона динамики (второго закона Ньютона) следует:
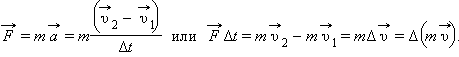 |
Физическая величина, равная произведению массы тела на скорость его движения, называется импульсом тела (или количеством движения). Импульс тела – векторная величина. Единицей измерения импульса в СИ является килограмм-метр в секунду (
Физическая величина, равная произведению силы на время ее действия, называется импульсом силы. Импульс силы также является векторной величиной.
В новых терминах второй закон Ньютона может быть сформулирован следующим образом: изменение импульса тела (количества движения) равно импульсу силы.
Обозначив импульс тела буквой 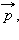 второй закон Ньютона можно записать в виде
второй закон Ньютона можно записать в виде
|
Именно в таком общем виде сформулировал второй закон сам Ньютон. Сила 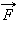 в этом выражении представляет собой равнодействующую всех сил, приложенных к телу. Это векторное равенство может быть записано в проекциях на координатные оси:
в этом выражении представляет собой равнодействующую всех сил, приложенных к телу. Это векторное равенство может быть записано в проекциях на координатные оси:

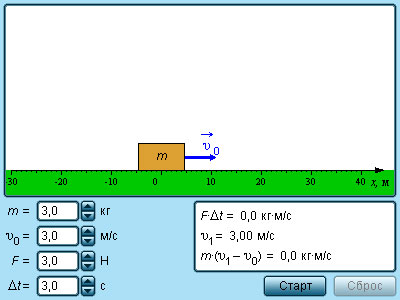 |
Модель. Импульс тела |
Таким образом, изменение проекции импульса тела на любую из трех взаимно перпендикулярных осей равно проекции импульса силы на эту же ось. Рассмотрим в качестве примера одномерное движение, т. е. движение тела по одной из координатных осей (например, оси
Этот простой результат совпадает с кинематической формулой для скорости равноускоренного движения. В этом примере сила оставалась неизменной по модулю на всем интервале времени
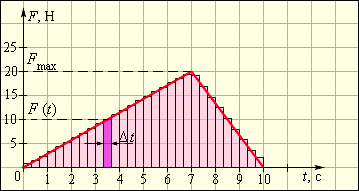 |
| Рисунок 1.16.1. Вычисление импульса силы по графику зависимости |
Выберем на оси времени малый интервал
Импульс силы, график которой представлен на рис. 1.16.1, на интервале от
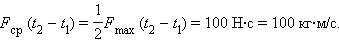 |
В этом простом примере 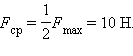
В некоторых случаях среднюю силу
Импульс
Следовательно, средняя сила
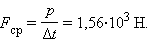 |
Это очень большая сила. Она приблизительно равна весу тела массой
Если движение тела во время действия силы происходило по некоторой криволинейной траектории, то начальный 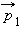 и конечный
и конечный 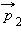 импульсы тела могут отличаться не только по модулю, но и по направлению. В этом случае для определения изменения импульса
импульсы тела могут отличаться не только по модулю, но и по направлению. В этом случае для определения изменения импульса 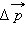 удобно использовать диаграмму импульсов, на которой изображаются вектора
удобно использовать диаграмму импульсов, на которой изображаются вектора 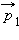 и
и 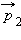 , а также вектор
, а также вектор 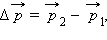 построенный по правилу параллелограмма. В качестве примера на рис. 1.16.2 изображена диаграмма импульсов для мяча, отскакивающего от шероховатой стенки. Мяч массой
построенный по правилу параллелограмма. В качестве примера на рис. 1.16.2 изображена диаграмма импульсов для мяча, отскакивающего от шероховатой стенки. Мяч массой 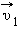 под углом
под углом 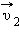 под углом
под углом  направление которой совпадает с направлением вектора
направление которой совпадает с направлением вектора 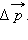
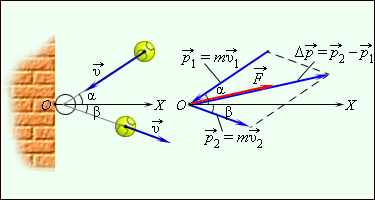 |
| Рисунок 1.16.2. Отскок мяча от шероховатой стенки и диаграмма импульсов |
При нормальном падении мяча массой 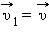 после отскока мяч будет иметь скорость
после отскока мяч будет иметь скорость 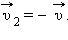 Следовательно, изменение импульса мяча за время отскока равно
Следовательно, изменение импульса мяча за время отскока равно 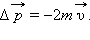 В проекциях на ось
В проекциях на ось