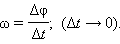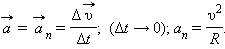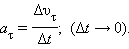1.6. Движение по окружности
Движение тела по окружности является частным случаем криволинейного движения. Наряду с вектором перемещения 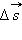 удобно рассматривать угловое перемещение
удобно рассматривать угловое перемещение
При малых углах поворота
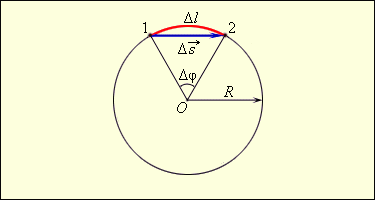 |
| Рисунок 1.6.1. Линейное 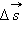 и угловое и угловое 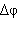 перемещения при движении тела по окружности перемещения при движении тела по окружности |
Угловой скоростью
|
Угловая скорость измеряется в рад/с.
Связь между модулем линейной скорости
При равномерном движении тела по окружности величины 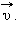
Равномерное движение тела по окружности является движением с ускорением. Ускорение
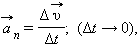 |
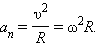 |
Для доказательства этого выражения рассмотрим изменение вектора скорости 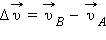 за малый промежуток времени
за малый промежуток времени
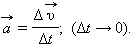 |
Векторы скоростей 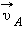 и
и 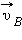 в точках
в точках
Из подобия треугольников
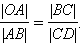 |
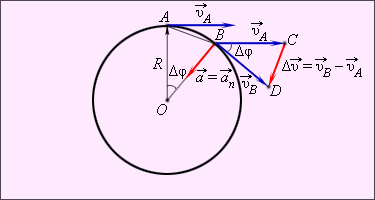 |
| Рисунок 1.6.2. Центростремительное ускорение тела 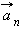 при равномерном движении по окружности при равномерном движении по окружности |
При малых значениях угла
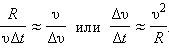 |
При малых углах 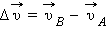 приближается к направлению на центр окружности. Следовательно, переходя к пределу при
приближается к направлению на центр окружности. Следовательно, переходя к пределу при
|
При изменении положения тела на окружности изменяется направление на центр окружности. При равномерном движении тела по окружности модуль ускорения остается неизменным, но направление вектора ускорения изменяется со временем. Вектор ускорения в любой точке окружности направлен к ее центру. Поэтому ускорение при равномерном движении тела по окружности называется центростремительным.
В векторной форме центростремительное ускорение может быть записано в виде
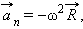 |
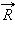 – радиус-вектор точки на окружности, начало которого находится в ее центре.
– радиус-вектор точки на окружности, начало которого находится в ее центре.
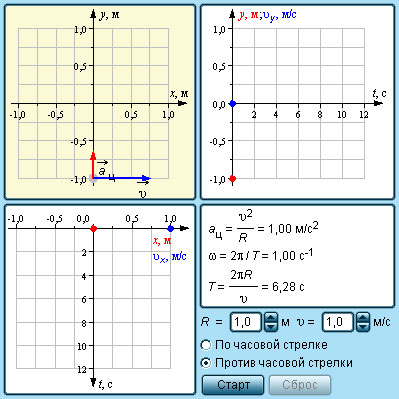 |
Модель. Равномерное движение по окружности |
Если тело движется по окружности неравномерно, то появляется также касательная (или тангенциальная) составляющая ускорения (см. §1.1):
|
В этой формуле
Направление вектора полного ускорения 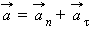 определяется в каждой точке круговой траектории величинами нормального и касательного ускорений (рис. 1.6.3).
определяется в каждой точке круговой траектории величинами нормального и касательного ускорений (рис. 1.6.3).
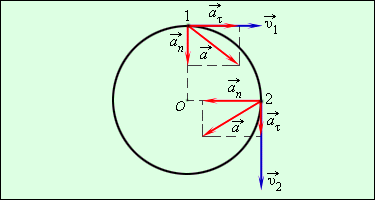 |
| Рисунок 1.6.3. Составляющие ускорения 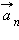 и и 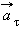 при неравномерном движении тела по окружности при неравномерном движении тела по окружности |
Движение тела по окружности можно описывать с помощью двух координат
При равномерном вращении тела величины
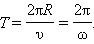 |
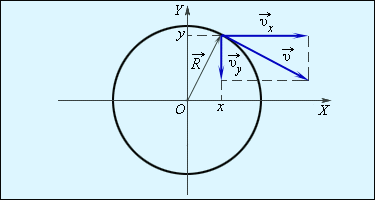 |
| Рисунок 1.6.4. Разложение вектора скорости 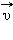 по координатным осям по координатным осям |